My reserach field consists in defining and developing new methods and tools in the environment of HPC numerical simulation codes. More precisely, I focus my research on the generation and manipulation of meshes for numerical simulation purposes.. It can be divided into three main areas:
- The generation of quadrilateral and hexahedral meshes
- Partitioning of graphs and meshes
- The adaptation of meshes into hybrid concurrent and distributed parallelism.
This activity is carried out in close collaboration with the IBISC laboratory at the University of Evry-Val-d’Essonne (Paris-Saclay), where I have been an associate professor (PAST) in Computer Science since 2009.
Proceedings of the 2024 International Meshing Roundtable (IMR), 2024

abstract

Abstract
Computational analysis with the finite element method requires geometrically accurate meshes. It is well known that high-order meshes can accurately capture curved surfaces with fewer degrees of freedom in comparison to low-order meshes. Existing techniques for high-order mesh generation typically output meshes with same polynomial order for all elements. However, high order elements away from curvilinear boundaries or interfaces increase the computational cost of the simulation without increasing geometric accuracy. In prior work [5, 21], we have presented one such approach for generating body-fitted uniform-order meshes that takes a given mesh and morphs it to align with the surface of interest prescribed as the zero isocontour of a level-set function. We extend this method to generate mixed-order meshes such that curved surfaces of the domain are discretized with high-order elements, while low-order elements are used elsewhere. Numerical experiments demonstrate the robustness of the approach and show that it can be used to generate mixed-order meshes that are much more efficient than high uniform-order meshes. The proposed approach is purely algebraic, and extends to different types of elements (quadrilaterals/triangles/tetrahedron/hexahedra) in two- and three-dimensions.
SIAM IMR24-SIAM International Meshing Roundtable Workshop, 2024

abstract
Abstract
This work aims to provide a method to generate block-structured meshes suitable for Computational Fluid Dynamics (CFD) simulations of flows around vehicles during atmospheric re-entry. This method takes as input a tetrahedral mesh of the domain, and the quadrangular block discretization of the vehicle surface. A linear blocking is obtained using an advancing front algorithm. This means it is incrementally created from the vehicle surface, layer by layer. Then, this linear blocking is curved, and we generate the final mesh. Some results of blocking and corresponding meshes generated with our algorithm are shown.
SIAM International Meshing Roundtable 2023, Springer Nature Switzerland, p. 43-63, 2023



abstract
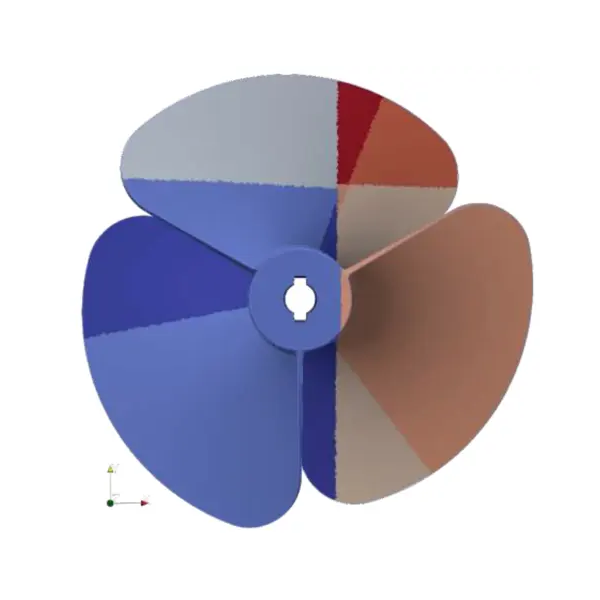
Abstract
This paper presents Coupe, a mesh partitioning platform. It provides solutions to solve different variants of the mesh partitioning problem, mainly in the context of load-balancing parallel mesh-based applications. From partitioning weights ensuring balance to topological partitioning that minimizes communication metrics through geometric methods, Coupe offers a large panel of algorithms to fit user-specific problems. Coupe exploits shared memory parallelism, is written in Rust, and consists of an open-source library and command line tools. Experimenting with different algorithms and parameters is easy. The code is available on Github.
Euro-Par 2022 International Workshops, Glasgow, UK, August 22–26, 2022, Revised Selected Papers, Glasgow, United Kingdom, 2023

abstract

Abstract
Mesh partitioning used for load balancing in distributed numerical simulations is typically managed with tools that are good enough but not optimal. Their use scope is not explicitly dedicated to load balancing, and they cannot make use of all available information. In this paper, the mesh partitioning problem and the context for its use are precisely defined. Then, existing tools are presented, along with their characteristics and features that are missing. Finally, a new partitioning platform – the subject of my PhD thesis – is presented: its architecture, software engineering choices made along the way, and how it can be the best fit for load balancing distributed simulations. The platform is open-source and is hosted on GitHub: https://github.com/LIHPC-Computational-Geometry/coupe .
Abstract
Quad meshing is a very well-studied domain for many years. Although the problem can generally be considered solved, many approaches do not provide adequate inputs for Computational Fluid Dynamics (CFD) and, in our case, hypersonic flow simulations. Such simulations require very strong monitoring of cell size and direction. To our knowledge, engineers do this manually with the help of interactive software. In this work we propose an automatic algorithm to generate full quadrilateral block structured mesh for the purpose of hypersonic flow simulation. Using this approach we can handle some simulation input like the angle of attack and the boundary layer definition. We will present here 2D results of computation on a hypersonic vehicle using the meshes generated by our method.
International Meshing Roundtable, 2023


abstract
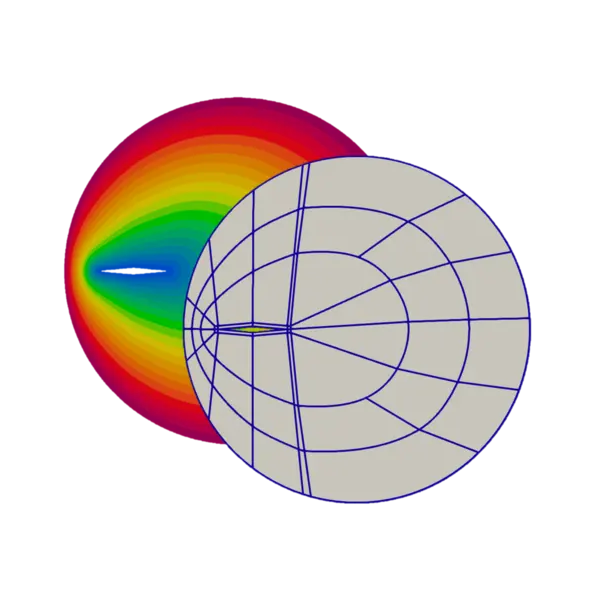
Abstract
Quad meshing is a very well-studied domain for many years. While the problem can be globally considered as solved, many approaches do not provide suitable inputs for Computational Fluid Dynamics (CFD) and in our case for supersonic flow simulations. Such simulations require a very strong control on the cell size and direction. To our knowledge, engineers ensure this control manually using interactive software. In this work we propose an automatic algorithm to generate full quadrilateral block structured mesh for the purpose of supersonic flow simulation. We handle some simulation input like the angle of attack and the boundary layer definition. Our approach generates adequate 2D meshes and is designed to be extensible in 3D.
SIAM International Meshing Roundtable, 2023

abstract
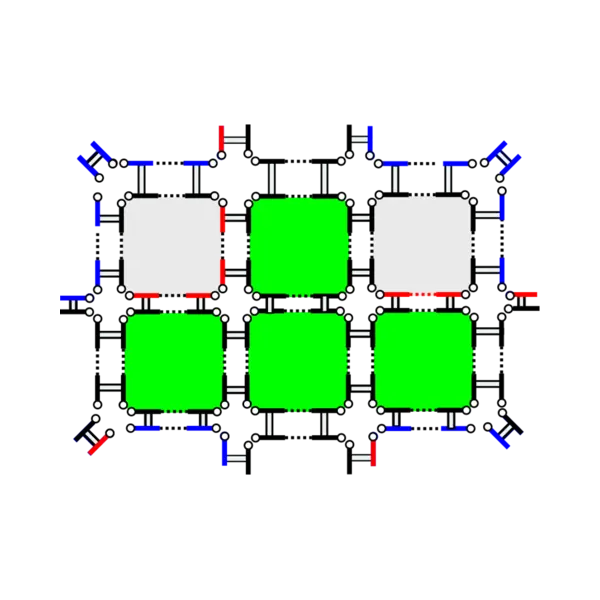
Abstract
Nowadays for real study cases, the generation of full block structured hexahedral meshes is mainly an interactive and very-time consuming process realized by highly-qualified engineers. To this purpose, they use interactive software where they handle and modify complex block structures with operations like block removal, block insertion, O-grid insertion, propagation of block splitting, propagation of meshing parameters along layers of blocks and so on. Such operations are error-prone and modifying or adding an operation is a very tedious work. In this work, we propose to formally define hexahedral block structures and main associated operations in the model of n-dimensional generalized map. This model provides topological invariant and a systematic handling of geometric data that allows us to ensure the expected robustness.

Abstract
Polycube-maps are used as base-complexes in various fields of computational geometry, including the generation of regular all-hexahedral meshes free of internal singularities. However, the strict alignment constraints behind polycube-based methods make their computation challenging for CAD models used in numerical simulation via finite element method (FEM). We propose a novel approach based on an evolutionary algorithm to robustly compute polycube-maps in this context. We address the labelling problem, which aims to precompute polycube alignment by assigning one of the base axes to each boundary face on the input. Previous research has described ways to initialize and improve a labelling via greedy local fixes. However, such algorithms lack robustness and often converge to inaccurate solutions for complex geometries. Our proposed framework alleviates this issue by embedding labelling operations in an evolutionary heuristic, defining fitness, crossover, and mutations in the context of labelling optimization. We evaluate our method on a thousand smooth and CAD meshes, showing Evocube converges to accurate labellings on a wide range of shapes. The limitations of our method are also discussed thoroughly.

Abstract
An important part of recent advances in hexahedral meshing focuses on the deformation of a domain into a polycube; the polycube deformed by the inverse map fills the domain with a hexahedral mesh. These methods are appreciated because they generate highly regular meshes. In this paper we address a robustness issue that systematically occurs when a coarse mesh is desired: algorithms produce deformations that are not one-to-one, leading to collapse of large portions of the model when trying to apply the (undefined) inverse map. The origin of the problem is that the deformation requires to perform a mixed integer optimization, where the difficulty to enforce the integer constraints is directly tied to the expected coarseness. Our solution is to introduce sanity constraints preventing the loss of bijectivity due to the integer constraints.
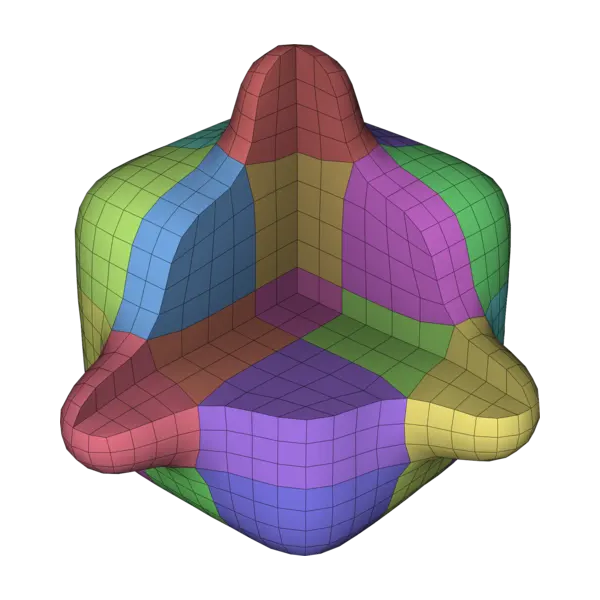
Abstract
In this article, we provide a detailed survey of techniques for hexahedral mesh generation. We cover the whole spectrum of alternative approaches to mesh generation, as well as post-processing algorithms for connectivity editing and mesh optimization. For each technique, we highlight capabilities and limitations, also pointing out the associated unsolved challenges. Recent relaxed approaches, aiming to generate not pure-hex but hex-dominant meshes, are also discussed. The required background, pertaining to geometrical as well as combinatorial aspects, is introduced along the way.

Abstract
Abstract HexMe consists of 189 tetrahedral meshes with tagged features and a workflow to generate them. The primary purpose of HexMe meshes is to enable consistent and practically meaningful evaluation of hexahedral meshing algorithms and related techniques, specifically regarding the correct meshing of specified feature points, curves, and surfaces. The tetrahedral meshes have been generated with Gmsh, starting from 63 computer-aided design (CAD) models from various databases. To highlight and label the diverse and challenging aspects of hexahedral mesh generation, the CAD models are classified into three categories: simple, nasty, and industrial. For each CAD model, we provide three kinds of tetrahedral meshes (uniform, curvature-adapted, and box-embedded). The mesh generation pipeline is defined with the help of Snakemake, a modern workflow management system, which allows us to specify a fully automated, extensible, and sustainable workflow. It is possible to download the whole dataset or select individual meshes by browsing the online catalog. The HexMe dataset is built with evolution in mind and prepared for future developments. A public GitHub repository hosts the HexMe workflow, where external contributions and future releases are possible and encouraged. We demonstrate the value of HexMe by exploring the robustness limitations of state-of-the-art frame-field-based hexahedral meshing algorithm. Only for 19 of 189 tagged tetrahedral inputs all feature entities are meshed correctly, while the average success rates are 70.9% / 48.5% / 34.6% for feature points/curves/surfaces.
Mesh Generation and Adaptation: Cutting-Edge Techniques, Springer International Publishing, p. 69-94, 2022

abstract
Abstract
In this chapter, we deal with the problem of mesh conversion for coupling lagrangian and eulerian simulation codes. More specifically, we focus on hexahedral meshes, which are known as pretty difficult to generate and handle. Starting from an eulerian hexahedral mesh, i.e. a hexahedral mesh where each cell contains several materials, we provide a full-automatic process that generates a lagrangian hexahedral mesh, i.e. a hexahedral mesh where each cell contains a single material. This process is simulation-driven in the meaning that the we guarantee that the generated mesh can be used by a simulation code (minimal quality for individual cells), and we try and preserve the volume and location of each material as best as possible. In other words, the obtained lagrangian mesh fits the input eulerian mesh with high-fidelity. To do it, we interleave several advanced meshing treatments--mesh smoothing, mesh refinement, sheet insertion, discrete material reconstruction, discrepancy computation, in a fully integrated pipeline. Our solution is evaluated on 2D and 3D examples representative of CFD simulation (Computational Fluid Dynamics).
2020 Proceedings of the SIAM Workshop on Combinatorial Scientific Computing, p. 85-95, 2020

abstract
Abstract
Running numerical simulations on HPC architectures requires distributing data to be processed over the various available processing units. This task is usually done by partitioning tools, whose primary goal is to balance the workload while minimizing inter-process communication. However, they do not take the memory load and memory capacity of the processing units into account. As this can lead to memory overflow, we propose a new approach to address mesh partitioning by including ghost cells in the memory usage and by considering memory capacity as a strong constraint to abide. We model the problem using a bipartite graph and present a new greedy algorithm that aims at producing a partition according to the memory capacity. This algorithm focuses on memory consumption, and we use it in a multi-level approach to improving the quality of the returned solutions during the refinement phase. The experimental results obtained from our benchmarks show that our approach can yield solutions respecting memory constraints for instances where traditional partitioning tools fail.
Proceedings of the 28th International Meshing Roundtable, 2019

abstract
Abstract
Hexahedral mesh generation using overlay grid methods has the benefit of being fully automatic, requiring minimal user input. These methods follow a mesh-first approach where an initial mesh, usually a grid, is used to overlay the reference geometry. Procedures to modify the initial mesh are then employed to best capture the geometry to get a conformal all-hex mesh [1\]. One of the main drawbacks of those methods is the resulting mesh quality. While the interior of the mesh remains the same as the initial mesh, cells located at the material interfaces can end up quite deformed or even inverted, making the mesh totally useless for most numerical simulation codes. Considering an input mesh carrying volume fractions of the materials, the main purpose of the presented work is to ensure a minimal cell quality. Our method draws upon the overlay grid pipeline described in [2\] where several steps (cell assignment correction, interface reconstruction, mesh adaptation) are altered to control cell quality.
Dual-based user-guided hexahedral block generation using frame fields, 2019

abstract

Abstract
Block structured hexahedral meshing is required for many applications but remains unreachable in an automatic manner for realistic simulation models. In practice, true industrial cases are handled using complex and rich interactive software, and generating a block structure for a mechanical CAD part can require several days to weeks for an expert engineer. For many years now, several scientific works have demonstrated that 3D frame fields are a very powerful tool for hexahedral meshing. These works remain mainly theoretical and their application is limited to simple 3D models. In this paper, we propose to provide the necessary components to build an interactive tool using frame fields. The principle of the approach is to build a valid dual structure made of 3D dual sheets, which are aligned along a 3D frame field, and then to convert this dual structure into its primal hexahedral block structure.
Abstract
In this work, we provide a new post-processing procedure for automatically adjusting node locations of an all-hex mesh to better match the volume of a reference geometry. This process is particularly well-suited for mesh-first approaches, as overlay grid ones. In practice, hexahedral meshes generated via an overlay grid procedure, where a precise reference geometry representation is unknown or is impractical to use, do not provide for precise volumetric preservation. A discrete volume fraction representation of the reference geometry MI on an overlay grid is compared with a volume fraction representation of a 3D finite element mesh MO. This work introduces the notion of localized discrepancy between MI and MO and uses it to design a procedure that relocates mesh nodes to more accurately match a reference geometry. We demonstrate this procedure on a wide range of hexahedral meshes generated with the Sculpt code and show improved volumetric preservation while still maintaining acceptable mesh quality.
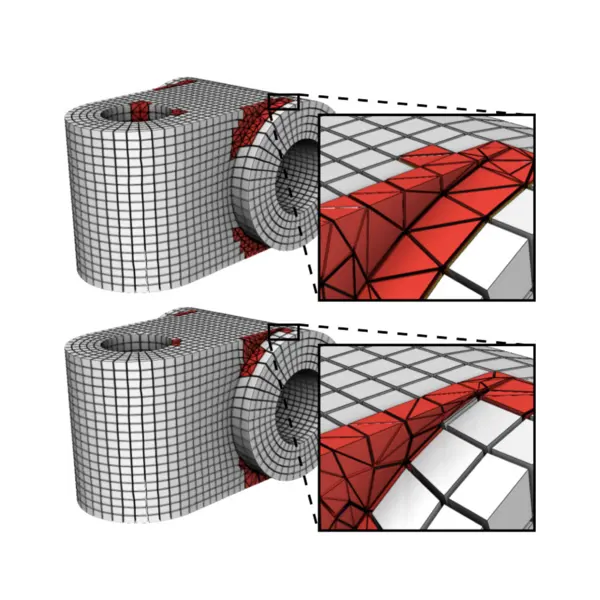
Abstract
We propose a robust pipeline that can generate hex-dominant meshes from any global parameterization of a tetrahedral mesh. We focus on robustness in order to be able to benchmark different parameterizations on a large database. Our main contribution is a new method that integrates the hexahedra (extracted from the parameterization) into the original object. The main difficulty is to produce the boundary of the result, composed of both faces of hexahedra and tetrahedra. Obviously, this surface must be a good approximation of the original object but, more importantly, it must be possible to remesh the volume bounded by this surface minus the extracted hexahedra (called void). We enforce these properties by carefully tracking and eliminating all possibilities of failure at each step of our pipeline. We tested our method on a large collection of objects (200+) with different settings. In most cases, we obtained results of very good quality as compared to the state-of-the-art solutions. To ease reproducing our results and benchmarks, we provide a C++ implementation of the pipeline in the supplemental materials.
Procedia Engineering, p. 258-270, 2017-01

abstract
Abstract
We propose a new post-processing procedure for automatically adjusting node locations of an all-hex mesh to better match the volume of a reference geometry. Hexahedral meshes generated via an overlay grid procedure, where a precise reference geometry representation is unknown or is impractical to use, do not provide for precise volumetric preservation. A discrete volume fraction representation of the reference geometry MI on an overlay grid is compared with a volume fraction representation of a 3D finite element mesh MO. This work proposes a procedure that uses the localized discrepancy between MI and MO to drive node relocation operations to more accurately match a reference geometry. We demonstrate this procedure on a wide range of hexahedral meshes generated with the Sculpt code and show improved volumetric preservation while still maintaining acceptable mesh quality.
Euro-Par 2017: Parallel Processing, Springer International Publishing, p. 594-606, 2017

abstract
Abstract
In this paper, we present a fine-grained multi-stage metric-based triangular remeshing algorithm on manycore and NUMA architectures. It is motivated by the dynamically evolving data dependencies and workload of such irregular algorithms, often resulting in poor performance and data locality at high number of cores. In this context, we devise a multi-stage algorithm in which a task graph is built for each kernel. Parallelism is then extracted through fine-grained independent set, maximal cardinality matching and graph coloring heuristics. In addition to index ranges precalculation, a dual-step atomic-based synchronization scheme is used for nodal data updates. Despite its intractable latency-boundness, a good overall scalability is achieved on a NUMA dual-socket Intel Haswell and a dual-memory Intel KNL computing nodes (64 cores). The relevance of our synchronization scheme is highlighted through a comparison with the state-of-the-art.

Abstract
Recent methods for frame field generation in two and three dimensions are reviewed. Frame fields generated automatically in 2D and 3D are analyzed with respect to quad and hex mesh generation. Problems are identified with automatically generated frame fields that prevent mesh generation via current methods. Specifically, there exist geometries that contain limit cycles and cannot be parameterized or decomposed by separatrices of the frame field. In 3D, singularity lines occur that minimize the field curvature but do not align with the frame field. These types of singularities make it impossible to create a mesh that both follows the frame field, and simultaneously respects the singularity as an irregular node in the mesh. Specific examples are presented that illustrate these problems. For each example, streamlines are used to help visualize properties of the frame fields, problems are analyzed, and options to potentially mitigate such problems are discussed.
Proceedings of the 21st International Meshing Roundtable, Springer Berlin Heidelberg, p. 315-332, 2013

abstract
Abstract
Generating a full hexahedral mesh for any 3D geometric domain is still a challenging problem. Among the different attempts, the octree-based methods are the most efficient from an engineering point of view. But the main drawback of such methods is the lack of control near the boundary. In this work, we propose an a posteriori technique based on the notion of the fundamental mesh in order to improve the mesh quality near the boundary. This approach is based on the resolution of a constraint problem defined on the topology of the CAD model that we have to discretize.
Proceedings of the 6th International Conference on Adaptive Modeling and Simulation, ADMOS 2013, p. 412-422, 2013

abstract
Abstract
In numerous computational engineering applications, hexahedral meshes may be preferred over tetrahedral meshes. However, automatic hexahedral meshing remains an unsolved issue and thus generating a hexahedral mesh is known as a time-consuming stage that requires a lot of user interactions in the simulation process. A possible way for designing and optimizing a CAD model or a geometric shape requires parametric studies where the shape is enriched by inserting geometric details into it. Then we must \"adapt\" the initial mesh and not generate it anew for each new detail taken into account. In order to perform such studies with hexahedral meshes, we provide an imprinting method allowing us to automatically add geometric details into an existing mesh. This addition is done using geometric projections, sheets (layers of hexahedral elements) insertions and combinatorial algorithms while preserving the hexahedral mesh structure as best as possible.
p. 1279-1293, 2010

abstract

Abstract
Abstract This paper presents a new method, called Mesh Matching, for handling non-conforming hexahedral-to-hexahedral interfaces for finite element analysis. Mesh Matching modifies the hexahedral element topology on one or both sides of the interface until there is a one-to-one pairing of finite element nodes, edges and quadrilaterals on the interface surfaces, allowing mesh entities to be merged into a single conforming mesh. Element topology is modified using hexahedral dual operations, including pillowing, sheet extraction, dicing and column collapsing. The primary motivation for this research is to simplify the generation of unstructured all-hexahedral finite element meshes. Mesh Matching relaxes global constraint propagation which currently hinders hexahedral meshing of large assemblies, and limits its extension to parallel processing. As a secondary benefit, by providing conforming mesh interfaces, Mesh Matching provides an alternative to artificial constraints such as tied contacts and multi-point constraints. The quality of the resultant conforming hexahedral mesh is high and the increase in number of elements is moderate. Copyright © 2009 John Wiley & Sons, Ltd.




