Nicolas is a member of the meshing team that focuses on hexahedral mesh generation, with an emphasis on block-structured meshes used in simulation codes.
He contributes to the open-source software (gmds and mgx) of the team and to the supervision of students; he has defended a PhD while in post between 2017 and 2020.
Prior to his activities at CEA he has worked as an INRIA associate engineer being part of the HPC R&D (parallelism and performance optimization) in a simulation code.
SIAM International Meshing Roundtable, 2023

abstract
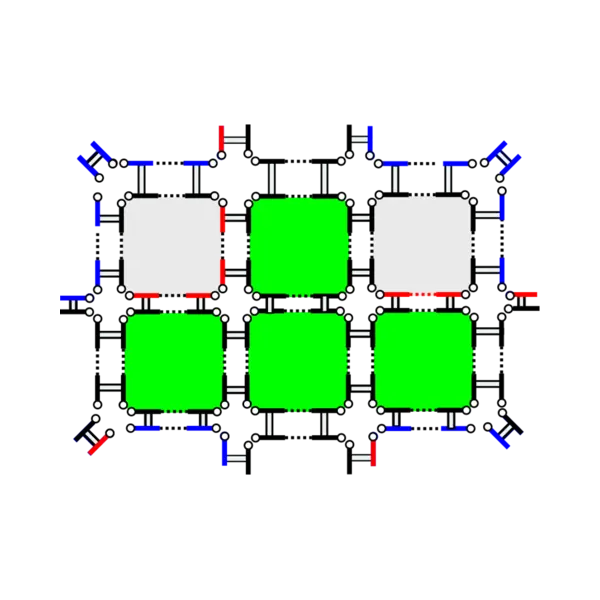
Abstract
Nowadays for real study cases, the generation of full block structured hexahedral meshes is mainly an interactive and very-time consuming process realized by highly-qualified engineers. To this purpose, they use interactive software where they handle and modify complex block structures with operations like block removal, block insertion, O-grid insertion, propagation of block splitting, propagation of meshing parameters along layers of blocks and so on. Such operations are error-prone and modifying or adding an operation is a very tedious work. In this work, we propose to formally define hexahedral block structures and main associated operations in the model of n-dimensional generalized map. This model provides topological invariant and a systematic handling of geometric data that allows us to ensure the expected robustness.
Mesh Generation and Adaptation: Cutting-Edge Techniques, Springer International Publishing, p. 69-94, 2022

abstract
Abstract
In this chapter, we deal with the problem of mesh conversion for coupling lagrangian and eulerian simulation codes. More specifically, we focus on hexahedral meshes, which are known as pretty difficult to generate and handle. Starting from an eulerian hexahedral mesh, i.e. a hexahedral mesh where each cell contains several materials, we provide a full-automatic process that generates a lagrangian hexahedral mesh, i.e. a hexahedral mesh where each cell contains a single material. This process is simulation-driven in the meaning that the we guarantee that the generated mesh can be used by a simulation code (minimal quality for individual cells), and we try and preserve the volume and location of each material as best as possible. In other words, the obtained lagrangian mesh fits the input eulerian mesh with high-fidelity. To do it, we interleave several advanced meshing treatments--mesh smoothing, mesh refinement, sheet insertion, discrete material reconstruction, discrepancy computation, in a fully integrated pipeline. Our solution is evaluated on 2D and 3D examples representative of CFD simulation (Computational Fluid Dynamics).
université Paris-Saclay, 2020

abstract
Abstract
This thesis addresses the problem of the automatic generation of purely hexahedral meshes for simulation codes when having a mesh carrying volume fraction data as an input, meaning that there can be several materials inside one cell. The proposed approach should create an hexahedral mesh where each cell corresponds to a single material, and where interfaces between materials form smooth surfaces. From a theoretical standpoint, we aim at adapting and extending state-of-the-art techniques and we apply them on examples, some classically issued from CAD models (and imprinted onto a mesh to obtain volume fractions), some procedurally generated cases and others in an intercode capacity where we take the results of a first simulation code to be our inputs. We first define a metric that allows the evaluation of our (or others') results and a method to improve those; we then introduce a discrete material interface reconstruction method inspired from the scientific visualization field and finally we present an algorithmic pipeline, called {sc ELG}, that offers a guarantee on the mesh quality by performing geometrical and topological mesh adaptation.
Proceedings of the 28th International Meshing Roundtable, 2019

abstract
Abstract
Hexahedral mesh generation using overlay grid methods has the benefit of being fully automatic, requiring minimal user input. These methods follow a mesh-first approach where an initial mesh, usually a grid, is used to overlay the reference geometry. Procedures to modify the initial mesh are then employed to best capture the geometry to get a conformal all-hex mesh [1\]. One of the main drawbacks of those methods is the resulting mesh quality. While the interior of the mesh remains the same as the initial mesh, cells located at the material interfaces can end up quite deformed or even inverted, making the mesh totally useless for most numerical simulation codes. Considering an input mesh carrying volume fractions of the materials, the main purpose of the presented work is to ensure a minimal cell quality. Our method draws upon the overlay grid pipeline described in [2\] where several steps (cell assignment correction, interface reconstruction, mesh adaptation) are altered to control cell quality.
Abstract
In this work, we provide a new post-processing procedure for automatically adjusting node locations of an all-hex mesh to better match the volume of a reference geometry. This process is particularly well-suited for mesh-first approaches, as overlay grid ones. In practice, hexahedral meshes generated via an overlay grid procedure, where a precise reference geometry representation is unknown or is impractical to use, do not provide for precise volumetric preservation. A discrete volume fraction representation of the reference geometry MI on an overlay grid is compared with a volume fraction representation of a 3D finite element mesh MO. This work introduces the notion of localized discrepancy between MI and MO and uses it to design a procedure that relocates mesh nodes to more accurately match a reference geometry. We demonstrate this procedure on a wide range of hexahedral meshes generated with the Sculpt code and show improved volumetric preservation while still maintaining acceptable mesh quality.
Procedia Engineering, p. 258-270, 2017-01

abstract
Abstract
We propose a new post-processing procedure for automatically adjusting node locations of an all-hex mesh to better match the volume of a reference geometry. Hexahedral meshes generated via an overlay grid procedure, where a precise reference geometry representation is unknown or is impractical to use, do not provide for precise volumetric preservation. A discrete volume fraction representation of the reference geometry MI on an overlay grid is compared with a volume fraction representation of a 3D finite element mesh MO. This work proposes a procedure that uses the localized discrepancy between MI and MO to drive node relocation operations to more accurately match a reference geometry. We demonstrate this procedure on a wide range of hexahedral meshes generated with the Sculpt code and show improved volumetric preservation while still maintaining acceptable mesh quality.
Euro-Par 2017: Parallel Processing, Springer International Publishing, p. 594-606, 2017

abstract
Abstract
In this paper, we present a fine-grained multi-stage metric-based triangular remeshing algorithm on manycore and NUMA architectures. It is motivated by the dynamically evolving data dependencies and workload of such irregular algorithms, often resulting in poor performance and data locality at high number of cores. In this context, we devise a multi-stage algorithm in which a task graph is built for each kernel. Parallelism is then extracted through fine-grained independent set, maximal cardinality matching and graph coloring heuristics. In addition to index ranges precalculation, a dual-step atomic-based synchronization scheme is used for nodal data updates. Despite its intractable latency-boundness, a good overall scalability is achieved on a NUMA dual-socket Intel Haswell and a dual-memory Intel KNL computing nodes (64 cores). The relevance of our synchronization scheme is highlighted through a comparison with the state-of-the-art.
Proceedings of the 21st International Meshing Roundtable, Springer Berlin Heidelberg, p. 315-332, 2013

abstract
Abstract
Generating a full hexahedral mesh for any 3D geometric domain is still a challenging problem. Among the different attempts, the octree-based methods are the most efficient from an engineering point of view. But the main drawback of such methods is the lack of control near the boundary. In this work, we propose an a posteriori technique based on the notion of the fundamental mesh in order to improve the mesh quality near the boundary. This approach is based on the resolution of a constraint problem defined on the topology of the CAD model that we have to discretize.
Proceedings of the 6th International Conference on Adaptive Modeling and Simulation, ADMOS 2013, p. 412-422, 2013

abstract
Abstract
In numerous computational engineering applications, hexahedral meshes may be preferred over tetrahedral meshes. However, automatic hexahedral meshing remains an unsolved issue and thus generating a hexahedral mesh is known as a time-consuming stage that requires a lot of user interactions in the simulation process. A possible way for designing and optimizing a CAD model or a geometric shape requires parametric studies where the shape is enriched by inserting geometric details into it. Then we must \"adapt\" the initial mesh and not generate it anew for each new detail taken into account. In order to perform such studies with hexahedral meshes, we provide an imprinting method allowing us to automatically add geometric details into an existing mesh. This addition is done using geometric projections, sheets (layers of hexahedral elements) insertions and combinatorial algorithms while preserving the hexahedral mesh structure as best as possible.
Geophysical Journal International, p. 721-739, 2011-08

abstract
Abstract
We present forward and adjoint spectral-element simulations of coupled acoustic and (an)elastic seismic wave propagation on fully unstructured hexahedral meshes. Simulations benefit from recent advances in hexahedral meshing, load balancing and software optimization. Meshing may be accomplished using a mesh generation tool kit such as CUBIT, and load balancing is facilitated by graph partitioning based on the SCOTCH library. Coupling between fluid and solid regions is incorporated in a straightforward fashion using domain decomposition. Topography, bathymetry and Moho undulations may be readily included in the mesh, and physical dispersion and attenuation associated with anelasticity are accounted for using a series of standard linear solids. Finite-frequency Fréchet derivatives are calculated using adjoint methods in both fluid and solid domains. The software is benchmarked for a layercake model. We present various examples of fully unstructured meshes, snapshots of wavefields and finite-frequency kernels generated by Version 2.0 'Sesame' of our widely used open source spectral-element package SPECFEM3D.
High Performance Computing for Computational Science - VECPAR, Springer, p. 350-363, 2008

abstract
Abstract
In order to better understand the internal structure of asteroids orbiting in the Solar system and then the response of such objects to impacts, seismic wave propagation in asteroid 433-Eros is performed numerically based on a spectral-element method at frequencies lying between 2 Hz and 22 Hz. In the year 2000, the NEAR Shoemaker mission to Eros has provided images of the asteroid surface, which contains numerous fractures that likely extend to its interior. Our goal is to be able to propagate seismic waves resulting from an impact in such models. For that purpose we create and mesh both homogeneous and fractured models with a highly-dispersive regolith layer at the surface using the CUBIT mesh generator developed at Sandia National Laboratories (USA). The unstructured meshes are partitioned using the METIS software package in order to minimize edge cuts and therefore optimize load balancing in our parallel blocking or non-blocking MPI implementations. We show the results of several simulations and illustrate the fact that they exhibit good scaling.
SC '08: Proceedings of the 2008 ACM/IEEE Conference on Supercomputing, p. 1-11, 2008-11

abstract
Abstract
SPECFEM3D_GLOBE is a spectral element application enabling the simulation of global seismic wave propagation in 3D anelastic, anisotropic, rotating and self-gravitating Earth models at unprecedented resolution. A fundamental challenge in global seismology is to model the propagation of waves with periods between 1 and 2 seconds, the highest frequency signals that can propagate clear across the Earth. These waves help reveal the 3D structure of the Earth's deep interior and can be compared to seismographic recordings. We broke the 2 second barrier using the 62K processor Ranger system at TACC. Indeed we broke the barrier using just half of Ranger, by reaching a period of 1.84 seconds with sustained 28.7 Tflops on 32K processors. We obtained similar results on the XT4 Franklin system at NERSC and the XT4 Kraken system at University of Tennessee Knoxville, while a similar run on the 28K processor Jaguar system at ORNL, which has better memory bandwidth per processor, sustained 35.7 Tflops (a higher flops rate) with a 1.94 shortest period.Thus we have enabled a powerful new tool for seismic wave simulation, one that operates in the same frequency regimes as nature; in seismology there is no need to pursue periods much smaller because higher frequency signals do not propagate across the entire globe.We employed performance modeling methods to identify performance bottlenecks and worked through issues of parallel I/O and scalability. Improved mesh design and numbering results in excellent load balancing and few cache misses. The primary achievements are not just the scalability and high teraflops number, but a historic step towards understanding the physics and chemistry of the Earth's interior at unprecedented resolution.





